La vitesse et la hauteur
Lorsque l’on réalise une mesure de la vitesse du vent, il faut toujours indiquer à quelle hauteur au-dessus du sol cette mesure a été effectuée. Imaginons que vous essayez d’estimer le potentiel éolien existant sur un terrain donné, plus particulièrement à un emplacement donné de ce terrain. Vous réalisez une campagne de mesure durant laquelle vous placez un mât de mesure qui fait 20 m de hauteur. Et bien, les vitesses de vent que vous allez rencontrer à cette hauteur sont différentes de ce que vous mesureriez à 30 ou 50 m.
Cette caractéristique est assez importante dans la mesure où, en début de projet, vous ne connaissez pas encore la hauteur du mât à laquelle vous allez placer votre éolienne. Du coup, vous ne savez pas à quelle hauteur il y a lieu de réaliser votre mesure. En fait, c’est exactement la situation opposée : vous réalisez une campagne de mesure pour savoir à quelle hauteur vous devez placer votre éolienne.
Quel phénomène physique se cache derrière tout cela ? Dans le jargon de la mécanique des fluides, on appelle ce phénomène une couche limite. Parler de ce phénomène est relativement complexe et lourd, c’est pourquoi nous allons simplifier grandement son explication pour introduire les conclusions d’intérêt pour notre développement.
Si l’on se place à une certaine hauteur au-dessus du sol, le vent possède une certaine vitesse que nous appellerons Vr (pour vitesse de référence). Au niveau sol, c’est-à-dire l’air qui touche le sol, la vitesse du vent est nulle. Ce phénomène est induit par la viscosité de l’air. La vitesse du vent va donc progresser de zéro au niveau du sol à la vitesse Vr que nous avons mesurée à une certaine hauteur. Cette progression entre ces deux vitesses se fera de manière plus ou moins régulière, avec des augmentations voire des diminutions locales de vitesse, suivant l’historique du vent, c’est-à-dire les obstacles que le vent a rencontrés avant d’arriver au point que l’on analyse ainsi que les modifications qu’il a subies. En outre, la rugosité du sol a une influence sur l’évolution de la vitesse en fonction de la hauteur. En d’autres termes, la vitesse ne progresse pas de la même manière suivant que le sol soit en gazon ou recouvert de plantations. On pourrait croire que c’est complètement farfelu, voire improbable, mais il est possible de la justifier physiquement, ce que nous ne ferons pas, et l’expérience le prouve clairement.
L’évolution peut être très complexe et, de manière générale, il n’existe aucune méthode simple pour pouvoir prédire cette évolution de la vitesse en fonction de la hauteur. Si on ne peut extrapoler la vitesse mesurée à une autre altitude, il faut alors réaliser la mesure à une hauteur proche de ce que sera la future éolienne.
Heureusement, le comportement du vent se simplifie un peu dans certains cas particuliers. Et c’est souvent dans ces configurations particulières que l’on placera une éolienne. Du coup, des solutions pour déduire le vent à différentes hauteurs existent.
Terrains plats et homogènes : les lois de puissance
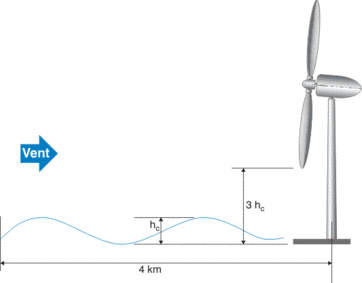
Lorsque le sol ne présente pas de variations de relief importantes comparées à la hauteur de la future éolienne et ce, dans un rayon de plusieurs dizaines de fois cette hauteur, on peut qualifier ce terrain de « plat« . L’évolution de la vitesse de vent au voisinage du sol évoluera de manière relativement lente et progressive au fur et à mesure que le vent parcourt le terrain.
Cette évolution restera progressive si la couverture de sol, essentiellement sa rugosité, n’évolue pas dans cette zone de rayon de plusieurs dizaines de fois la hauteur. On dira que le terrain est « homogène« .
Si l’éolienne se situe sur un terrain plat, homogène et sans obstacle alors le vent évolue de manière progressive sans être perturbé. Il rentre alors dans un régime plus standard dans lequel des lois permettent de déduire l’évolution de la vitesse en fonction de la hauteur. Et encore, il ne s’agit pas de n’importe quelle vitesse, mais d’une vitesse moyenne. Cette moyenne n’a rien avoir avec les moyennes introduites aux sections précédentes qui se réalisaient sur des périodes de plusieurs mois voire un an. Il s’agit maintenant de considérer des moyennes sur des échelles de temps de quelques minutes. En effet, le vent est de nature turbulente si bien que la vitesse fluctue de manière continuelle autour d’une certaine moyenne. De manière très simplifiée, on peut dire que la turbulence ajoute un certain bruit de fond à l’évolution temporelle de la vitesse. Ce que les lois simplifiées proposent d’évaluer ici est l’évolution de la moyenne de la vitesse (où les fluctuations induites par la turbulence ont été filtrées) en fonction de la hauteur au dessus du sol. On peut illustrer cette distinction avec les deux figures ci-dessous, la première montrant un champ instantané et la seconde la moyenne.

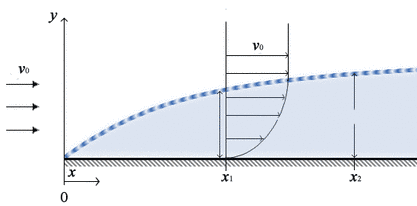
Comparaison entre la visualisation expérimentale d’une couche limite turbulente comprenant un grand nombre de fluctuations (première figure) et l’évolution de la vitesse moyenne en fonction la hauteur (seconde figure). Les règles que l’on donne ici concernent uniquement l’évolution de la vitesse moyenne avec la hauteur pour les terrains plats, homogènes et sans obstacles.
La plus connue est la loi de puissance. Son fondement théorique est souvent mis en question, mais cette approche s’avère souvent utile sur le terrain ou dans les applications de l’ingénieur. Si on mesure à la hauteur de référence, hr, une vitesse, Vr, on peut déduire la vitesse V(h) rencontrée à une autre hauteur, h :
V(h) = Vr*(h/hr)α,
le seul paramètre à fixer étant le coefficient « α », dit coefficient de cisaillement. En fait, celui-ci dépend essentiellement de la rugosité du sol (ou de la couverture du sol si vous préférez) :
| Terrain |
Exposant de cisaillement du vent, α |
| Glace |
0.07 |
| Neige sur terrain plat |
0.09 |
| Mer calme |
0.09 |
| Gazon coupé |
0.14 |
| Gazon court type prairie |
0.16 |
| Gazon long type cultures céréales |
0.19 |
| Haies |
0.21 |
| Arbres et haies clairsemés |
0.24 |
| Arbres et haies plus denses |
0.29 |
| Banlieue |
0.31 |
| Forêt |
0.43 |
Exposant de cisaillement du vent en fonction de la rugosité du sol (pour une hauteur de référence de 10 m).
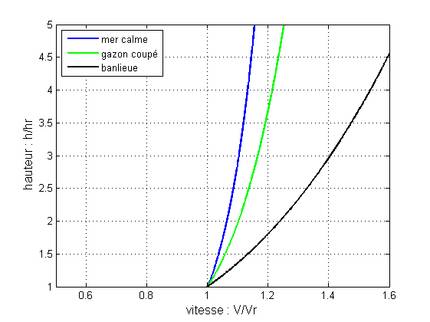
Puissance du vent et hauteur
Prenons pour exemple un terrain avec du gazon coupé caractérisé par un coefficient « α » de 0.14. Si on réalise une mesure, une vitesse de 5 m/s à une hauteur de 10 m, alors la vitesse du vent à 20 m sera de 5*(20/10)0.14 soit de 5.5 m/s, une augmentation de 10 %. Comme on sait que la puissance du vent dépend du cube de la vitesse, on a Pv(h) = Pv(hr)*(h/hr)3α. La puissance aura, elle, augmenté de 34 %. Si on augmente la hauteur du mât d’un facteur 5, c’est-à-dire en le plaçant à 50 m, alors la vitesse augmente de 25 % et la puissance du vent double. Cela met clairement en évidence que la hauteur du mât à une très grande importance. Il faut toujours placer son éolienne suffisamment haut, dans le cas contraire, on risque d’avoir des rendements déplorables. Pour les petites éoliennes domestiques, une hauteur de 10m est un minimum.
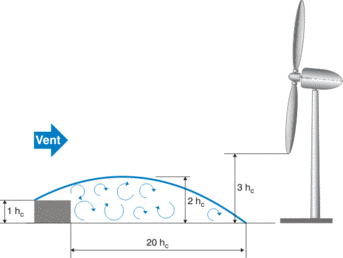
Obstacle ou rugosité ?
Pour conclure cette section, il faut être prudent dans l’emploi d’un tel tableau et de la loi de puissance associée. En effet, le lecteur attentif aura remarqué que l’on a considéré des haies ou les arbres comme étant des obstacles, mais aussi dans le tableau ci-dessus comme étant simplement de la rugosité du sol. Finalement, quand faut-il considérer un objet comme de la rugosité ou comme un obstacle ? En fait, comme évoqué plus haut, un obstacle doit avoir une taille comparable à l’éolienne tandis que la rugosité doit être composée d’une multitude d’éléments petits par rapport à la taille de l’éolienne (pouvant être considérés comme étant des aspérités du sol). À titre d’exemple, si on place une éolienne dans une clairière entourée de forêt, les arbres sont des obstacles pour une petite éolienne et sont des éléments de rugosité pour une grande éolienne commerciale.
Couche limite et charge sur le rotor
Nous avons mis en évidence que la vitesse augmente avec la hauteur par rapport au sol. Cela a un impact évident sur l’énergie du vent qui sera récupérée par l’éolienne. On ne le répétera jamais assez, mais il faut que celle-ci soit placée suffisamment haut pour assurer la rentabilité, la viabilité du projet. Le choix de la hauteur de mât est donc de première importance.
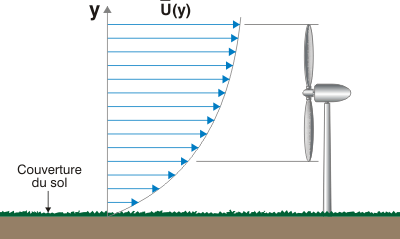
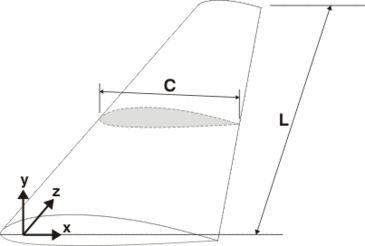
Illustration d’un chargement asymétrique sur le rotor par le vent.
Un autre aspect lié à l’évolution de la vitesse avec la hauteur est la charge aérodynamique sur le rotor. Si l’on place le rotor de l’éolienne trop bas, il recevra comme annoncé un vent plus faible, mais cette vitesse risque en plus de varier significativement le long du rotor. En d’autres termes, les forces exercées par le vent seront plus importantes sur les pales pointées sur le haut que sur les pales pointées vers le bas. Du coup, le rotor est soumis à une contrainte mécanique de nature asymétrique (différence haut-bas) et fluctuante (le rotor passe de la position basse à la position haute). Ces contraintes ont un impact négatif sur la durée de vie du matériel.