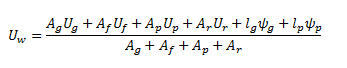Coefficient de transmission thermique (paroi) Archives

Coefficient de transmission thermique d’une façade légère de type mur rideau

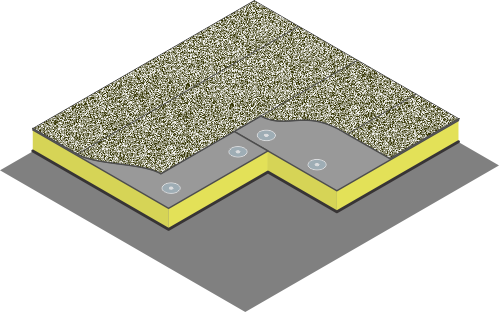
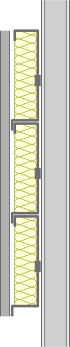
Les façades de ce type sont constituées de vitrages, de châssis et de panneaux opaques comme les fenêtres mais sont assemblés dans des structures pour former des modules. L’ensemble de ces modules compose la façade légère.

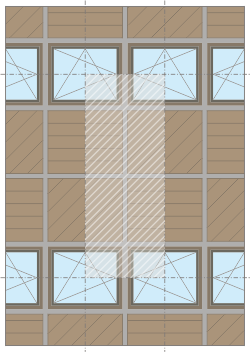
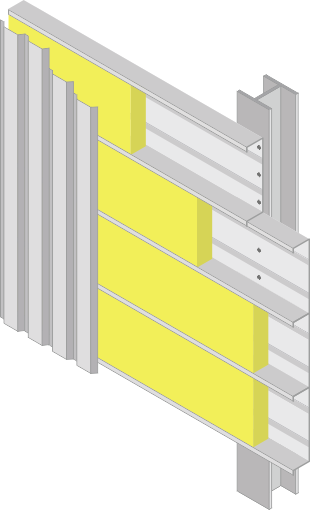
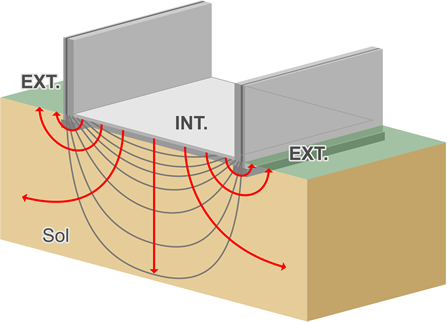
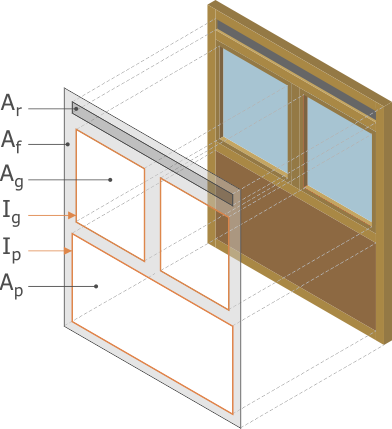
Exemple de module de façade légère :

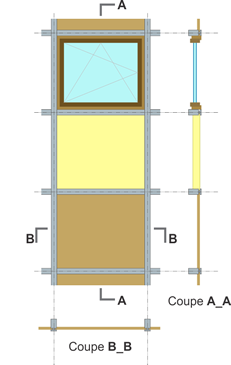
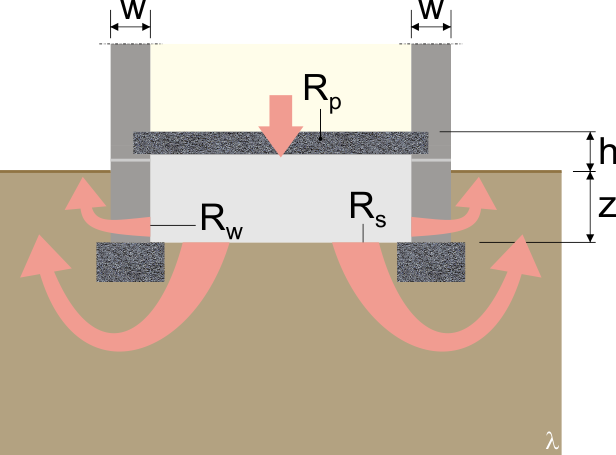
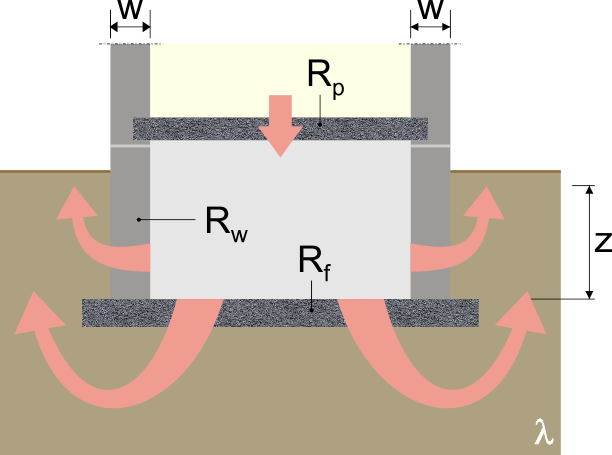
La présence de la structure constituée généralement de meneaux (verticaux) et de traverses (horizontales) assurant la fixation et la stabilité de l’ensemble provoque des ponts thermiques supplémentaires dont il faudra tenir compte pour évaluer les performances thermiques de la façade légère.

Détermination précise du coefficient de transmission thermique U_cw,tot par calcul numérique

Une façade légère peut être partagée en différents modules dont certains sont identiques. Les plans de coupe sont choisis de telle sorte qu’ils délimitent des parties de façade ayant un coefficient de transmission thermique U_cw,i propre. La valeur globale U_cw,tot de l’entièreté de la façade légère est la moyenne pondérée par les aires des valeurs U de tous les modules qui compose la façade légère.

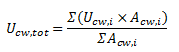
avec :

A_cw,i = les aires des différents modules (m²)
U_cw,i = les coefficients de transmission thermique des différents modules (W/m²K)

Détermination précise du coefficient de transmission thermique de la valeur U_cw,i par essais

Le coefficient de transmission thermique U_cw,i d’un module de façade légère peut être déterminé avec précision avant pose par des essais réalisés conformément à la norme NBN EN ISO 12567-1. Ils peuvent aussi être réalisés sur exactement le même module de façade légère avec les mêmes dimensions et les mêmes composants.

Détermination précise de la valeur U_cw,i par calcul numérique

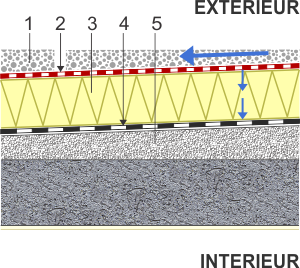
Un module de façade légère est constitué de différentes parties qui ont chacune une surface et un coefficient de transmission thermique U déterminés:

les encadrements (châssis),
le ou les vitrages,
le ou les panneaux opaques,
les meneaux,
les traverses.

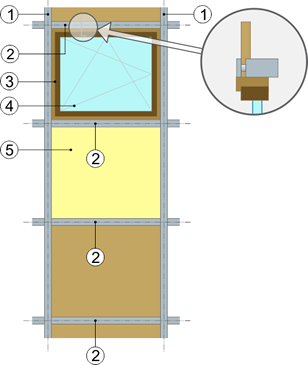
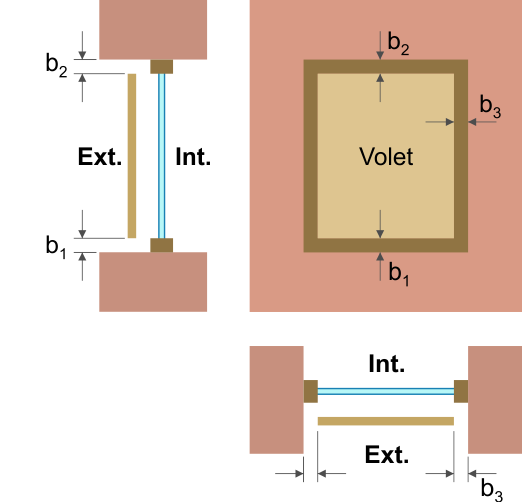
De plus, le contour des vitrages isolants et des panneaux est affecté d’une déperdition thermique supplémentaire résultant des effets combinés des encadrements, intercalaires, traverses, meneaux vitrages et panneaux (pont thermique linéaire).

L’ensemble de ces éléments permet de déterminer par calcul le coefficient de transmission thermique d’un module U_cw,i. Il s’agit de la valeur moyenne des coefficients de transmission thermique des différentes parties au pro rata de leurs surfaces, augmentées des déperditions linéiques aux rives des vitrages et panneaux et entre les châssis et les éléments de structure.

Sous forme mathématique simple cela s’écrit :

avec :

A_cw = l’aire totale du module de la façade légère
U_g = les coefficients de transmission thermique des différents vitrages
A_g = les aires des différents vitrages
U_f = les coefficients de transmission thermique des différents châssis (encadrements)
A_f = les aires des différents châssis (encadrements)
U_p = les coefficients de transmission thermique des différents panneaux
A_p = les aires des différents panneaux
U_m(t) = les coefficients de transmission thermique des différents meneaux et traverses
A_m(t) = les aires des différents meneaux et traverses
Ψ_f,g = les coefficients de transmission thermique linéique entre les différents vitrages et châssis (encadrements)
l_g = les périmètres visibles des différents vitrages dans les châssis (encadrements)
ψ_p = les coefficients de transmission thermique linéique autour des différents panneaux
l_g = les périmètres visibles des différents panneaux
Ψ_m(t),g = les coefficients de transmission thermique linéique entre les différents vitrages et les différents meneaux et traverses de la structure
l_m(t),g = les périmètres visibles des différents vitrages dans les différents meneaux et traverses de la structure
Ψ_m(t),f = les coefficients de transmission thermique linéique entre les différents châssis (encadrements) et les différents meneaux et traverses de la structure
l_m(t),f = les périmètres visibles des différents châssis (encadrements) dans les différents meneaux et traverses de la structure

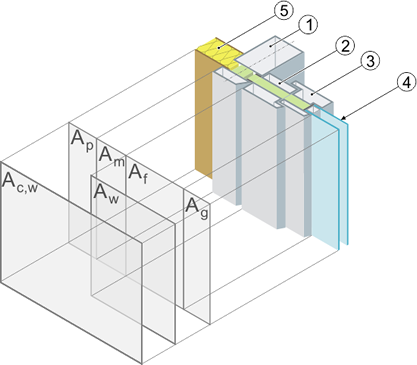
Les aires et périmètres sont déterminés conformément à l’Art. 10.2.2 de l’Annexe VII de l’AGW du 17 avril 2008.

Les coefficients de transmission thermique linéique ψ peuvent être déterminés à partir :

d’un calcul numérique précis suivant la norme NBN EN ISO 10077-2 ;
de valeurs par défaut mentionnées dans l’annexe E de l’AGW du 17 avril 2008 (Tableaux E2 , E3, E4, E5 et E6).

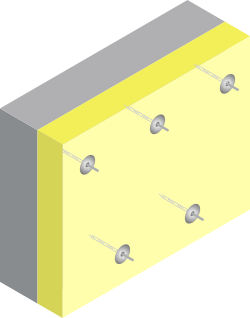
Influence des liaisons métalliques

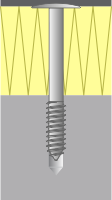
Le calcul numérique ne tient pas compte des ponts thermiques provoqués par les liaisons métalliques (vis) dans les traverses et meneaux. Ces ponts thermiques peuvent être calculés précisément suivant la NBN EN ISO 10211 ou par essais suivant la NBN EN 12412-2.

Il existe également une méthode simplifiée pour tenir compte de l’influence des vis sur le coefficient de transmission thermique Um(t) des meneaux et traverses. Ainsi pour des vis en acier inoxydable inter-distantes de 20 à 30 cm, le coefficient de transmission thermique est augmenté de 0.3 W/m²K. (Méthode de calcul suivant l’annexe C de la NBN EN 13947).

Source: AGW du 17 avril 2008, Annexe VII, Art 10.

Posted By : Sylvie 18 Mai, 2011

Influence de l’écoulement d’eau sous l’isolant des toitures inversées

L’écoulement de l’eau entre l’isolant d’une toiture inversée et la membrane d’étanchéité provoque une diminution des performances thermiques de l’isolant. La chaleur s’échappe en partie en réchauffant l’eau qui s’écoule.

Lestage,
Natte de protection,
Isolant,
Membrane d’étanchéité,
Support en pente.

La réglementation prévoit une procédure pour tenir compte de l’impact de l’écoulement lorsque la couche isolante est en polystyrène extrudé (XPS).
Un terme correctif ΔU_r est utilisé

U_c (U corrigé de la paroi) = U + ΔU_r.

ΔU_r est déterminé à partir des caractéristiques suivantes :

la quantité moyenne des précipitations pendant la saison de chauffe (en mm/jour) ;
le type de lestage (ouvert, appliqué en usine ou toiture verte) ;
la forme des bords des plaques (droits ou à rainures) ;
la résistance thermique corrigée de la couche d’isolant humidifié par diffusion ;
la résistance thermique totale de la paroi sans correction.

La formule du terme correctif ΔU_r est indiquée à l’Art 7.2.4 de l’Annexe B1 de l’AGW du 15 mai 2014 (formule 13).

Certaines valeurs par défaut peuvent être utilisées :

Précipitation moyenne : 2 mm/jour ;
Facteur de correction pour le transfert de chaleur par précipitation :
- 0.04 si plaques à bords droits et lestage ouvert ou appliqué en usine,
- 0.03 si plaques à rainures et lestage ouvert ou appliqué en usine,
- 0.02 si toiture verte.

Résistance thermique corrigée de l’isolant (XPS)
- R_XPS/1.023 si lestage ouvert ou appliqué en usine,
- R_XPS/1.069 si toiture verte.

Le logiciel PEB permet d’appliquer automatiquement les valeurs par défaut sur base des informations fournies.

Source : AGW du 15 mai 2014, Annexe B1, Art 7.2.4

Posted By : Sylvie 18 Mai, 2011

Influence des fixations mécaniques traversant l’isolant sur le coefficient de transmission thermique U

Lorsque la couche isolante d’une paroi est traversée par des fixations mécaniques (exemples : crochets de maçonnerie, fixations de couverture, …), la présence de celles-ci influence les performances thermiques de la paroi. La chaleur peut en effet s’échapper plus facilement en passant par les fixations généralement métalliques dont la conductivité thermique est beaucoup plus élevée que celle de l’isolant (exemple : acier : 50 000 W/mK <-> XPS : 0.040 W/mK). Heureusement leur section et leur nombre sont généralement réduits.

Crochets de maçonnerie.

Fixations mécaniques toiture chaude.

Calcul précis

L’impact des fixations sur les performances thermiques de la paroi peut toujours être évalué de manière précise par des calculs numériques conformes à la norme NBN EN ISO 10211.
Cette méthode précise de calcul doit toujours être utilisée si les deux extrémités des fixations mécaniques sont en contact thermique avec des plaques en métal (exemple : paroi à ossature métallique avec finitions métalliques sur les deux faces).

Méthode simplifiée

L’impact de la fixation mécanique sur le coefficient de transmission thermique U de la paroi peut être pris en compte par un terme correctif ΔU_f.

U_c (U corrigé de la paroi) = U + ΔU_f.

ΔU_f est déterminé à partir des caractéristiques suivantes :

la longueur de la partie de la fixation qui se trouve dans l’isolant ;
l’épaisseur de l’isolant ;
le nombre de fixations par m² ;
la section de la fixation ;
la conductivité thermique de l’isolant ;
la résistance thermique de la couche d’isolant traversée ;
la résistance thermique totale de la paroi sans les corrections.

L’introduction de ces informations dans le logiciel PEB, fourni gratuitement par la Région wallonne et la Région de Bruxelles-Capitale, permet le calcul automatique du terme correctif qui est alors appliqué directement au coefficient de transmission thermique U de la paroi.
La formule du terme correctif ΔUf est indiquée à l’Art 7.2.3 de l’Annexe B1 de l’AGW du 15 mai 2014 (formule 12).

Cas particulier des crochets de murs

1. Le terme correctif ΔUf ne doit pas être appliqué,

lorsque les crochets se trouvent dans des vides non isolés ;
lorsque les crochets ont une conductivité thermique λ inférieure à 1 W/mK (exemple : matière synthétique).

2. Il est toujours permis d’utiliser les valeurs par défaut suivantes

nombre de crochets par m² : 5 ;
section du crochet : 13 mm² (Ø 4 mm) ;
λ du crochet : 50 W/mK (acier) ;
longueur du crochet = épaisseur de l’isolant.

Le logiciel PEB permet d’appliquer automatiquement les valeurs par défaut.

Source: AGW du 15 mai 2014, Annexe B1, Art 7.2.3

Posted By : Sylvie 18 Mai, 2011

Coefficient de transfert thermique par transmission vers l’environnement extérieur via un espace adjacent non chauffé (EANC)

N.B.: Il s’agit ici d’un local situé au-dessus du sol et non d’une cave entièrement ou partiellement enterrée.

Le transfert de chaleur entre le bâtiment chauffé et l’extérieur au travers d’un espace adjacent non chauffé s’effectue aussi bien par transmission que par ventilation. Avant d’atteindre l’extérieur, la chaleur doit traverser les parois situées entre le volume protégé et l’EANC, l’EANC lui-même et encore les parois qui séparent l’EANC de l’environnement extérieur.

On tiendra donc compte pour le calcul de ces déperditions via une zone tampon non chauffée d’un coefficient de réduction de température b. Celui-ci intervient notamment dans la vérification des performances de la paroi par rapport aux exigences réglementaires :

U_max≥ b*U_eq

U_max ≥ b*1/R_T

Avec :

b : coefficient de réduction de température
R_T : la résistance thermique totale de la paroi considérée.

Calcul Précis

Le coefficient de réduction de température b peut être calculé avec précision en effectuant un équilibre thermique entre d’une part les déperditions entre l’espace chauffé et l’EANC et d’autre part entre l’EANC et l’environnement extérieur.

Dans le cadre de la réglementation PEB, le calcul détaillé se fait à l’aide de formules indiquées dans l’AGW du 15 mai 2014, Annexe B1, Art 14.

Les données nécessaires pour le calcul sont :

la résistance thermique et la surface de toutes les parois qui séparent l’espace chauffé de l’EANC
la résistance thermique et la surface de toutes les parois qui séparent l’EANC de l’environnement extérieur
le volume de l’EANC
un taux conventionnel de ventilation de l’EANC défini à partir de ses caractéristiques: n_ue. Ce taux conventionnel est déterminé à partir du tableau 6 de l’Art 14 de l’Annexe B1 de l’AGW du 15 mai 2014.

Le débit d’air de ventilation entre l’espace chauffé et l’EANC est conventionnellement fixé à 0 dans le cadre de la réglementation PEB.

L’introduction de ces informations dans le logiciel PEB, permet le calcul automatique du coefficient de transmission thermique de chaque paroi multiplié par son facteur de réduction thermique (b.U_i).

Calcul simplifié

Il est toujours possible de ne pas prendre en compte la présence des EANC. Dans ce cas le facteur de réduction thermique est égal à 1, ce qui est fortement pénalisant puisque cela revient à considérer que la paroi est en contact direct avec l’extérieur.

Source : AGW du 15 mai 2014, Annexe B1, Art 14

Posted By : Sylvie 18 Mai, 2011

Coefficient de transmission thermique moyen d’un plancher sur vide sanitaire

Un plancher au-dessus d’un vide sanitaire n’a pas de contact direct avec le sol, mais un flux de déperdition de chaleur s’échappe via ce vide sanitaire et via le sol vers l’environnement extérieur. Un transfert supplémentaire intervient si le vide sanitaire est ventilé avec de l’air extérieur.

Le sol participe donc à la résistance thermique du plancher (La chaleur, pour sortir du bâtiment et atteindre l’air extérieur, doit traverser le plancher, le vide sanitaire, les murs périphériques de celui-ci mais aussi le sol avec lequel il est en contact). On tiendra donc compte pour le calcul du transfert thermique à travers cette paroi d’un coefficient de réduction de température b. Celui-ci intervient notamment dans la vérification des performances de la paroi par rapport aux exigences réglementaires :

U_max≥ b * U_eq

U_max ≥ b*1/R_T

Avec :

b : coefficient de réduction de température
R_T : la résistance thermique totale de la paroi considérée.

Calcul Précis

Un calcul numérique précis de la transmission thermique peut se faire suivant des méthodes numériques conformes aux normes.

Procédure de calcul suivant la réglementation PEB

Le calcul détaillé se fait à l’aide de formules indiquées dans l’AGW, Annexe B1, Art F.2.3.
Les données nécessaires pour le calcul sont :

l’épaisseur du mur périphérique à la hauteur du niveau du sol;
la résistance thermique totale du mur périphérique ;
la profondeur moyenne du vide sanitaire sous le niveau du sol ;
le périmètre exposé du plancher SUR vide sanitaire ;
la surface du plancher SUR vide sanitaire ;
la résistance thermique totale du plancher SUR vide sanitaire ;
la hauteur moyenne du plancher SUR vide sanitaire au-dessus du sol extérieur ;
la résistance thermique de (l’éventuel) plancher SOUS le vide sanitaire ;
la surface des ouvertures de ventilation.

La conductivité thermique λ du sol, la vitesse du vent et le facteur de protection du vent sont définis par défaut dans le cadre de la réglementation PEB.

Calcul simplifié

La réglementation permet de déterminer le coefficient de transmission thermique équivalent Ueq multiplié par le facteur de réduction de température b, à l’aide d’une méthode simplifiée.

Elle donne une valeur de transmission thermique relativement pénalisante.

L’information nécessaire est la suivante :

le niveau de ventilation du vide sanitaire (peu ou pas ventilé ou bien très ventilé).

N.B.: L’introduction de cette information dans le logiciel PEB, fourni gratuitement par la Région wallonne et la Région de Bruxelles-Capitale, permet le calcul automatique du coefficient de transmission thermique équivalent multiplié par son facteur de réduction (b.U_eq).

Source: AGW du 15 mai 2014, Annexe B1, Art F.2.3 et Art 15.2.2

Posted By : Sylvie 18 Mai, 2011

Coefficient de transmission thermique moyen d’un plancher sur cave

Les caves sont des espaces qui se trouvent en partie ou totalement en dessous du niveau du sol extérieur.

Le sol participe à la résistance thermique du plancher (La chaleur, pour sortir du bâtiment et atteindre l’air extérieur, doit traverser le plancher, la cave, les murs périphériques et le plancher de celle-ci mais aussi le sol avec lequel ces parois sont en contact).

On tiendra donc compte pour le calcul du transfert thermique à travers le plancher sur cave d’un coefficient de réduction de température b. Celui-ci intervient notamment dans la vérification des performances de la paroi par rapport aux exigences réglementaires :

U_max≥ b * U_eq

U_max ≥ b * 1/R_T

Avec :

b : coefficient de réduction de température
R_T : la résistance thermique totale de la paroi considérée.

Calcul Précis

Un calcul numérique précis de la transmission thermique peut se faire suivant des méthodes numériques conformes aux normes.

Procédure de calcul suivant la réglementation PEB

Le calcul détaillé se fait à l’aide de formules indiquées dans l’AGW, Annexe B1, Art F.2.4.
Les données nécessaires pour le calcul sont :

l’épaisseur du mur périphérique à la hauteur du niveau du sol;
la résistance thermique totale du mur périphérique ;
la profondeur moyenne de la cave sous le niveau du sol ;
le périmètre exposé du plancher SUR la cave ;
la surface du plancher SUR la cave ;
la résistance thermique totale du plancher SUR la cave ;
le périmètre exposé du plancher SOUS la cave ;
la surface du plancher SOUS la cave ;
la résistance thermique totale du plancher SOUS la cave ;
la hauteur moyenne du plancher SUR vide sanitaire au-dessus du sol extérieur ;
la résistance thermique de (l’éventuel) plancher SOUS le vide sanitaire ;
le volume de la cave.

La conductivité thermique λ du sol et le taux de ventilation de la cave sont définis par défaut dans le cadre de la réglementation PEB.

Calcul simplifié

La réglementation permet de déterminer le coefficient de transmission thermique équivalent Ueq multiplié par le facteur de réduction de température b, à l’aide d’une méthode simplifiée.

Elle donne une valeur de transmission thermique relativement pénalisante.

Condition à remplir : au moins 70 % des parois de la cave doivent être en contact avec le sol.

L’information nécessaire est la suivante :

Y a-t-il ou pas des fenêtres ou des portes qui communiquent avec l’extérieur ?

Source: AGW du 15 mai 2014, Annexe B1, Art F.2.4 et Art 15.2.2

Posted By : Sylvie 18 Mai, 2011

Coefficient de transmission thermique moyen d’une dalle sur sol

Lorsqu’un local appartenant au volume protégé est limité par un plancher en contact avec le sol, la terre participe à la résistance thermique du plancher. La chaleur, pour sortir du bâtiment et atteindre l’air extérieur, doit traverser le plancher ainsi que le sol avec lequel il est en contact. Les isothermes (= lignes d’égale température) ne sont donc pas perpendiculaires au plan du plancher (comme c’est le cas lorsque le plancher est en contact avec l’extérieur) mais forment des courbes complexes.

Transmission de la chaleur à travers une dalle sur sol.

La méthode de calcul doit donc être adaptée. En pratique, on prendra en compte pour le calcul du transfert thermique un coefficient de réduction de température α. Celui-ci intervient notamment dans la vérification des performances de la paroi par rapport aux exigences réglementaires :

U_max≥ a * U_eq

U_max ≥ a * 1/R_T

Avec :

a : coefficient de réduction de température
R_T : la résistance thermique totale de la paroi considérée.

Calcul Précis

Un calcul numérique précis de la transmission thermique peut se faire suivant des méthodes numériques conformes aux normes.

Procédure de calcul suivant la réglementation PEB

Cette procédure est applicable lorsque le plancher est directement en contact avec le sol sur toute sa surface.

Le plancher peut être non-isolé, uniformément isolé ou isolé en partie (par exemple, isolation périphérique horizontale ou verticale.

Isolation périphérique horizontale.

Isolation périphérique verticale.

Le calcul détaillé se fait à l’aide de formules indiquées dans l’AGW, Annexe B1, Art F.2.2 (plancher directement en contact avec le sol) et Art F.2.4 (Parois d’une cave).

Les données nécessaires pour le calcul sont :

l’épaisseur du mur extérieur ;
le périmètre exposé du plancher ;
la surface du plancher ;
la résistance thermique totale du plancher ;

dans le cas d’une isolation périphérique sont également nécessaires :

la largeur de l’isolant (sa profondeur si elle est verticale) ;
l’épaisseur de l’isolant ;
la conductivité thermique de l’isolant ou sa résistance thermique ;

dans le cas d’un plancher situé plus bas que le niveau du sol extérieur :

la profondeur moyenne dans le sol ;
la résistance thermique totale du mur contre terre.

Les caractéristique du sol (conductivité thermique λ et facteur de nappe phréatique Gw) sont définies par défaut dans le cadre de la réglementation PEB.

Calcul simplifié

La réglementation permet de déterminer le coefficient de transmission thermique équivalent Ueq multiplié par le facteur de réduction de température α, à l’aide d’une méthode simplifiée: a=1/(Ueq + 1).

Elle donne une valeur de transmission thermique relativement pénalisante pour les grands bâtiments.

L’information nécessaire est la suivante :

la résistance thermique totale du plancher de l’environnement intérieur jusqu’à l’interface plancher-sol.

Source: AGW du 15 mai 2014, Annexe B1, Art F.2.2 et Art F.2.4 et Art 15.2.1

Posted By : Sylvie 18 Mai, 2011

Coefficient de transmission thermique moyen d’un mur contre terre

Lorsqu’un local appartenant au volume protégé est limité par un mur en contact avec le sol, l’environnement extérieur n’est plus l’air mais bien la terre. Celle-ci participe à la résistance thermique du mur. (La chaleur, pour sortir du bâtiment et atteindre l’air extérieur, doit traverser le mur mais aussi le sol qui l’entoure.) On tiendra donc compte pour le calcul du transfert thermique à travers cette paroi d’un coefficient de réduction de température α. Celui-ci intervient notamment dans la vérification des performances de la paroi par rapport aux exigences réglementaires :

U_max≥ a * U_eq

U_max ≥ a * 1/R_T

Avec :

a : coefficient de réduction de température
R_T : la résistance thermique totale de la paroi considérée.

Lorsqu’on considère un mur extérieur avec une structure homogène et une valeur U bien déterminée, les isothermes (= lignes d’égale température) seront toujours parallèles au plan de la façade et les lignes de flux de chaleur perpendiculaires à celui-ci.

Par contre, lorsque la chaleur doit traverser le sol qui entoure le bâtiment, les lignes de flux de chaleur forment des courbes et la méthode de calcul des valeurs U doit être adaptée.

Calcul Précis

Un calcul numérique précis de la transmission thermique peut se faire suivant des méthodes numériques conformes aux normes.

Procédure de calcul suivant la réglementation PEB

Le calcul détaillé se fait à l’aide de formules indiquées dans l’AGW, Annexe B1, Art F.2.4
Les données nécessaires pour le calcul sont :

l’épaisseur du mur extérieur à hauteur du sol ;
la résistance thermique totale du mur extérieur ;
la profondeur moyenne dans le sol ;
le périmètre exposé du plancher de la cave ;
la surface du plancher ;
la résistance thermique totale du plancher ;

Les caractéristiques du sol (conductivité thermique λ et facteur de nappe phréatique Gw) sont définies par défaut dans le cadre de la réglementation PEB.
L’introduction de ces informations dans le logiciel PEB permet le calcul automatique du coefficient de transmission thermique équivalent multiplié par son facteur de réduction (a.U_eq).

Calcul simplifié

Dans beaucoup de cas, il n’est pas nécessaire de faire appel à des calculs numériques et une méthode simplifiée peut être appliquée. Elle donne via l’application de certaines formules une valeur du coefficient de transmission thermique équivalent multiplié par son facteur de réduction (a.U_eq).

Le calcul se fait automatiquement en utilisant le logiciel PEB.

Les informations nécessaires sont les suivantes :

La hauteur moyenne de la partie du mur enterrée(z) ;
La résistance thermique du mur de l’environnement intérieur jusqu’à l’interface mur-sol (R_w).

Source: AGW du 15 mai 2014, Annexe B1, Art F.2.4 et Art 15.2.3

Posted By : Sylvie 13 Mai, 2011

Coefficient de transmission thermique des nœuds constructifs

Le coefficient de transmission thermique des nœuds constructifs

Les performances thermiques de nœuds constructifs sont caractérisées par le coefficient de transmission thermique linéaire Ψ (exprimé en W/mK) ou le coefficient de transmission thermique ponctuel χ (exprimé en W/K). Ces coefficients de transmission thermique indiquent quel supplément doit être ajouté au transport de chaleur qui a été calculé à partir des valeurs U.

Ψ et χ sont déduits des flux thermiques par transmission à l’endroit des nœuds déterminés exactement par des calculs numériques validés et comparés avec les flux thermiques calculés de manière unidimensionnelle.

On peut également utiliser des valeurs par défaut. Dans ce cas, il faut garder en mémoire que les valeurs par défaut sont particulièrement défavorables. L’utilisation systématique de valeurs par défaut sur l’ensemble d’un bâtiment conduira, dans la plupart des cas, à une pénalisation particulièrement élevée.

Prise en compte des nœuds constructifs dans le calcul de la performance énergétique des bâtiments suivant la réglementation PEB

Il s’agit du flux thermique qui se produira à travers tous les nœuds constructifs d’un volume protégé lorsqu’on applique une différence de température de 1 Kelvin entre le volume protégé et l’environnement extérieur.

La réglementation PEB prévoit trois options possibles pour déterminer ce flux thermique et son impact sur le niveau K.

Option A : Méthode détaillée

Avec cette option, le flux thermique est déterminé le plus exactement possible par un calcul numérique de l’influence des nœuds constructifs à l’aide d’un logiciel validé. On peut choisir de calculer le bâtiment dans son ensemble ou de calculer séparément chacun des nœuds constructifs. Ce genre de calcul nécessite beaucoup d’effort et sera principalement utilisé pour valoriser des nœuds constructifs très performants.

Option B : Méthode des nœuds correctement réalisés du point de vue thermique dits « nœuds PEB conformes »

Cette option a pour objectif de permettre la prise en compte des nœuds constructifs d’une manière pragmatique et simple. Des recherches sur les logements existants ont montré que l’influence de nœuds constructifs bien étudiés s’élevait à environ 3 points K sur le niveau K total d’un logement. Si on peut montrer que les nœuds constructifs sont effectivement bien étudiés (à savoir : PEB-conformes), alors un supplément forfaitaire équivalent à 3 points K est prévu pour ces nœuds constructifs. Les nœuds constructifs qui ne satisfont pas les critères sont comptabilisés séparément.

Un nœud est considéré comme PEB-conforme (dans l’option B), s’il répond au moins à une des conditions suivantes :

a) il respecte au moins une des règles de base :

épaisseur de contact suffisante entre les couches isolantes adjacentes (cf. figure 1).
critères s’appliquant sur des éléments isolants interposés (cf. figure 2).
longueur minimale du chemin de moindre résistance thermique (cf. figure 3).

b) son coefficient linéique de transmission thermique est plus petit qu’une valeur limite, définie en fonction du type de nœud (0,15 W/mK pour un angle rentrant, 0,1 W/mK pour les raccords autour des portes et fenêtre, p. ex.).

Fig.1 Épaisseur de contact minimale.

Fig.2 Interposition d’un isolant.

Fig.3 Schéma de principe du chemin de moindre résistance thermique.

Source : CSTC-Contact n° 27 (3-2010).

L’avantage de cette méthode est d’éviter des calculs conséquents et d’encourager les maîtres d’œuvre à concevoir des nœuds constructifs thermiquement performants. Vu que l’option B prévoit une possibilité de démontrer d’une manière simple et particulièrement visuelle qu’un nœud constructif est bien étudié, cette option a pour avantage que le calcul total pour la prise en compte des nœuds constructifs est réduit à un minimum. Il n’est pas nécessaire ici de déterminer les valeurs Ψ et χ, ni les longueurs des nœuds constructifs linéaires ou le nombre des nœuds constructifs ponctuels.

Option C : Pénalité forfaitaire (à éviter absolument)

Lorsque le maître d’œuvre ne fait pas d’effort pour limiter la déperdition thermique au droit des nœuds constructifs, l’influence inconnue des nœuds constructifs sur la déperdition thermique totale est fixée par un supplément forfaitaire équivalent à 10 points sur le niveau K est, dans ce cas, appliqué. Cette option doit être évitée, car elle aboutit à des bâtiments de mauvaise qualité et d’ailleurs oblige à porter plus d’effort d’isolation sur les parois pour atteindre les valeurs K exigées par la réglementation.

Attention !

Des nœuds constructifs mal étudiés ou mal réalisés thermiquement provoqueront des ponts thermiques. Le maître d’œuvre reste responsable de réduire au minimum absolu les risques de désordres dus à ces ponts thermiques (condensation, moisissures).

Posted By : olivier 24 Mar, 2011

Coefficient de transmission thermique d’une fenêtre (Uw) ou d’une porte

Le coefficient de transmission thermique d’une fenêtre ou d’une porte simple

N.B.: la méthode présentée ci-dessous n’est valable que pour les fenêtres ou portes considérées comme simples, cas le plus courant dans nos régions.

Elle ne s’applique pas à une double fenêtre ou à une fenêtre à vantaux dédoublés.

Fenêtre simple.

Double fenêtre.

Fenêtre à vantaux dédoublés.

Détermination par essais

Le coefficient de transmission thermique d’une porte ou d’une fenêtre peut être déterminé avant pose par des essais réalisés conformément à la norme NBN EN ISO 12567-1 (ou -2 pour une fenêtre de toit). Ils peuvent aussi être réalisés sur exactement la même fenêtre ou porte avec les mêmes dimensions et les mêmes composants.

Détermination par calcul

Une fenêtre ou une porte est constituée de différentes parties qui ont chacune une surface et un coefficient de transmission thermique U déterminés.

l’encadrement (châssis) de la fenêtre ou de la porte (dans tous les cas) ;
le ou les vitrages (le cas échéant) ;
le ou les panneaux opaques (le cas échéant) ;
la ou les grilles de ventilation (le cas échéant).

Le contour des vitrages isolants et des panneaux est affecté d’une déperdition thermique supplémentaire résultant des effets combinés des encadrements, intercalaires, vitrages et panneaux (pont thermique linéaire).

L’ensemble de ces éléments permet de déterminer par calcul le coefficient de transmission thermique de la fenêtre Uw. Il s’agit de la valeur moyenne des coefficients de transmission thermique des différentes parties au pro rata de leurs surfaces, augmentées des déperditions linéiques aux rives des vitrages et panneaux.

avec :

U_g = le coefficient de transmission thermique du vitrage
A_g = l’aire du vitrage
U_f = le coefficient de transmission thermique de l’encadrement
A_f = l’aire de l’encadrement
U_p = le coefficient de transmission thermique du panneau
A_p = l’aire du panneau
U_r = le coefficient de transmission thermique de la grille de ventilation
A_r = l’aire de la grille de ventilation
ψ_g = le coefficient de transmission thermique linéique de l’intercalaire autour du vitrage
l_g = le périmètre visible du vitrage
ψ_p = le coefficient de transmission thermique linéique autour du panneau
l_p = le périmètre visible du panneau

Le calcul doit être effectué pour chaque fenêtre et porte.

Calcul simplifié

Pour un ensemble de fenêtres ayant un même type de vitrage, d’encadrement, de panneau de remplissage opaque et de grille de ventilation, et étant placées dans le même bâtiment, on peut adopter une seule valeur moyenne UW pour l’ensemble des fenêtres. Celle-ci tient compte d’une proportion fixe entre l’aire du vitrage et l’aire de l’encadrement ainsi que d’un périmètre du vitrage ou des intercalaires. On évite ainsi de devoir faire ce calcul pour chaque fenêtre.

La réglementation PEB fournit ainsi une formule simplifiée permettant d’évaluer l’efficacité énergétique d’une fenêtre en tenant compte de l’efficacité du châssis et du vitrage tout en supposant une bonne étanchéité à l’air.

		Partie vitrage et encadrement	Partie grille de ventilation
U_g ≤ U_f	U_w	= 0,7U_g + 0,3U_f + 3ψ_g	+ ∑A_r (U_r – U_g)/∑A_W,d	[W/m²K]
U_g > U_f	U_w	= 0,8U_g + 0,2Uf + 3ψ_g	+ ∑A_r (U_r – U_f)/∑A_W,d	[W/m²K]

avec :

U_vc = coefficient de transmission thermique U du vitrage.
U_ch = coefficient de transmission thermique U du châssis.
ψ_g= coefficient de transmission thermique linéique de l’intercalaire.
U_r = coefficient de transmission thermique de la grille de ventilation
∑A_r = aire totale des grilles de ventilation présentes
∑A_W,d = aire totale des fenêtres (déterminée sur la base des aires des baies des fenêtres)

La proportion varie suivant que le vitrage est thermiquement plus performant que l’encadrement, ou l’inverse. Généralement c’est le vitrage qui est le plus performant. Dans ce cas la formule de calcul devient, s’il n’y a ni grille ni panneau :

U_W,T= 0,7 U_g+0,3 U_f+3 ψ_g

Ce qui revient à considérer : 70 % de vitrage, 30 % d’encadrement et 3 m d’intercalaire par m² de fenêtre.

Si la fenêtre comprend des grilles de ventilation et des panneaux opaques la formule se complique. Elle tient compte de l’influence de ces éléments sur le résultat final (pour les calculs, se référer aux formules 20 et 21 de l’Art 8.5 de l’Annexe 7).

Source : AGW du 15 mai 2014, Annexe B1, Art 8.5

L’influence du volet (Uws)

En été, la présence d’un volet à l’extérieur améliore les moyens dont dispose le bâtiment pour résister à la surchauffe.

En hiver, un volet placé à l’extérieur d’une fenêtre apporte une résistance thermique supplémentaire lorsqu’il est fermé. Bien sûr, il n’est pas fermé en permanence et le taux de fermeture variera d’une fenêtre à l’autre. La législation PEB en Belgique suppose qu’il sera fermé 8 heures par jour.

La résistance thermique de l’ensemble fenêtre-volet s’exprime de la manière suivante :

R_ws = R_w + ΔR

ΔR dépendra de deux caractéristiques :

La résistance thermique totale du volet lui-même, R_sh ;
La fente totale effective entre les bords du volet et les bords de l’ouverture du jour de la fenêtre b_sh = b₁ + b₂ + b₃ . b₁, b₂ et b₃ sont respectivement la moyenne des ouvertures des fentes en bas, en haut et sur les côtés du volet.

Attention, la fente sur le côté du volet (b3) n’est comptée qu’une fois parce que les fentes situées dans le haut et dans le bas ont une plus grande influence.

R_sh est calculé de la même manière que les autres éléments de construction.

Cas particuliers :

Le calcul se fait suivant la norme NBN EN ISO 10211 dans le cas d’un volet à composition hétérogène ;
Le calcul se fait suivant la norme NBN EN ISO 10077-2 dans le cas d’un élément profilé ;
Rsh = 0 dans le cas d’un volet inconnu.

Lorsque R_sh et b_sh sont déterminées, ΔR est calculé à partir des formules reprises dans le tableau 3 extrait de l’Art. 8.4.5 de l’Annexe B1 de l’AGW du 15 mai 2014.

Classe	Perméabilité à l’air du volet en position fermée	b_sh [mm]	ΔR [m²K/W]⁽¹⁾
1	Perméabilité très élevée	35 < b_sh	0,08
2	Perméabilité élevée (le volet est lui-même étanche à l’air).	15 < b_sh < 35	0,25 . R_sh + 0,09
3	Perméabilité moyenne (le volet est lui-même étanche à l’air)	8 < b_sh < 15	0,55 . R_sh + 0,11
4	Perméabilité faible (le volet est lui-même étanche à l’air).	b_sh < 8	0,80 . R_sh + 0,14
5	Perméabilité très faible (le volet est lui-même étanche à l’air).	b_sh < 3 et b₁ + b₃ = 0 ou₍₂₎ b₂₍₃₎ + b₃ = 0	0,95 . R_sh + 0,17
⁽¹⁾Les valeurs ΔR sont valables pour R_sh < 0,3 m²K/W (R_sh est la résistance thermique du volet même, déterminée selon le chapitre 6 si celui-ci est d’application, selon la NBN EN ISO 10211 dans le cas d’un volet à composition hétérogène ou selon la NBN ISO 10077-2 dans le cas d’un élément profilé). ⁽²⁾Ce cas suppose la présence de joints d’étanchéité autour d’au moins 3 côtés du volet et que du côté restant la fente soit inférieure ou égale à 3 mm. ⁽³⁾La classe 5 (perméabilité très faible) peut également être adoptée si une mesure du débit d’air au travers du volet fermé démontre que ce débit d’air n’est pas supérieur à 10 m³/h.m² (avec une différence de pression de 10 Pa – essai selon la NBN EN 12835. Des conditions supplémentaires pour la classe 5 sont disponibles dans la NBN EN 13125 par type de volet.

Tableau 3 : résistance thermique additionnelle de la couche d’air et du volet fermé.

ΔR étant ainsi connu, la résistance thermique de l’ensemble fenêtre volet Rws peut être calculée.
Le coefficient de conductivité thermique U_ws est finalement obtenu par la formule :

U_ws = 1 / R_ws

Le logiciel PEB permet de calculer automatiquement U_ws à partir des informations introduites.

Les caisses à volets roulants

Attention, la pose de volets suppose dans certains cas la présence de caisses à volets. Lorsqu’elles sont encastrées dans la façade, il faudra être très attentif à maintenir la continuité de la couche isolante et l’étanchéité à l’air du bâtiment. Cela n’est pas toujours facile. Les détails techniques doivent être étudiés avec soin dès de le début de la conception de l’immeuble.

Source: AGW du 15 mai 2014, Annexe B1, Art 8.4.5

Posted By : olivier 24 Mar, 2011

Coefficient de transmission thermique d’une paroi (U)

Généralités

Le coefficient de transmission thermique d’une paroi est la quantité de chaleur traversant cette paroi en régime permanent, par unité de temps, par unité de surface et par unité de différence de température entre les ambiances situées de part et d’autre de la paroi.
Le coefficient de transmission thermique est l’inverse de la résistance thermique totale (R_T) de la paroi.

U = 1 / R_T

> U (ou k) s’exprime en W/m²K
Plus sa valeur est faible et plus la construction sera isolée.

Pour calculer le coefficient U d’une paroi, rendez-vous sur la page « Calculs » – catégorie « Enveloppe » !

Category Archives: Coefficient de transmission thermique (paroi)

Détermination précise du coefficient de transmission thermique Ucw,tot par calcul numérique

Détermination précise du coefficient de transmission thermique de la valeur Ucw,i par essais

Détermination précise de la valeur Ucw,i par calcul numérique

Influence des liaisons métalliques

Calcul précis

Méthode simplifiée

Cas particulier des crochets de murs

Calcul Précis

Calcul simplifié

Calcul Précis

Procédure de calcul suivant la réglementation PEB

Calcul simplifié

Calcul Précis

Procédure de calcul suivant la réglementation PEB

Calcul simplifié

Calcul Précis

Procédure de calcul suivant la réglementation PEB

Calcul simplifié

Calcul Précis

Procédure de calcul suivant la réglementation PEB

Calcul simplifié

Le coefficient de transmission thermique des nœuds constructifs

Prise en compte des nœuds constructifs dans le calcul de la performance énergétique des bâtiments suivant la réglementation PEB

Option A : Méthode détaillée

Option B : Méthode des nœuds correctement réalisés du point de vue thermique dits « nœuds PEB conformes »

Option C : Pénalité forfaitaire (à éviter absolument)

Le coefficient de transmission thermique d’une fenêtre ou d’une porte simple

Détermination par essais

Détermination par calcul

Calcul simplifié

L’influence du volet (Uws)

Les caisses à volets roulants

Généralités

Détermination précise du coefficient de transmission thermique U_cw,tot par calcul numérique

Détermination précise du coefficient de transmission thermique de la valeur U_cw,i par essais

Détermination précise de la valeur U_cw,i par calcul numérique