24 mars 2011 - Energie Plus Le Site

Coefficient de transmission thermique d’une fenêtre (Uw) ou d’une porte

Le coefficient de transmission thermique d’une fenêtre ou d’une porte simple

N.B.: la méthode présentée ci-dessous n’est valable que pour les fenêtres ou portes considérées comme simples, cas le plus courant dans nos régions.

Elle ne s’applique pas à une double fenêtre ou à une fenêtre à vantaux dédoublés.

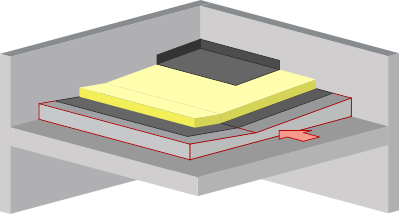
Fenêtre simple.

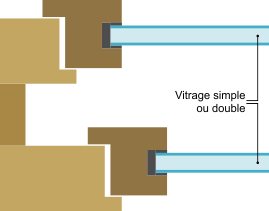
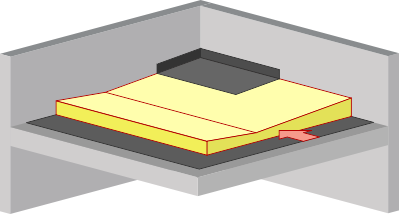
Double fenêtre.

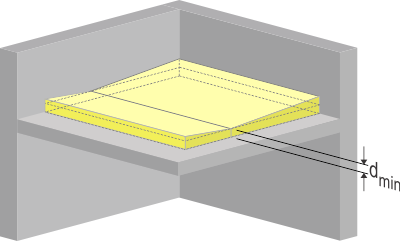
Fenêtre à vantaux dédoublés.

Détermination par essais

Le coefficient de transmission thermique d’une porte ou d’une fenêtre peut être déterminé avant pose par des essais réalisés conformément à la norme NBN EN ISO 12567-1 (ou -2 pour une fenêtre de toit). Ils peuvent aussi être réalisés sur exactement la même fenêtre ou porte avec les mêmes dimensions et les mêmes composants.

Détermination par calcul

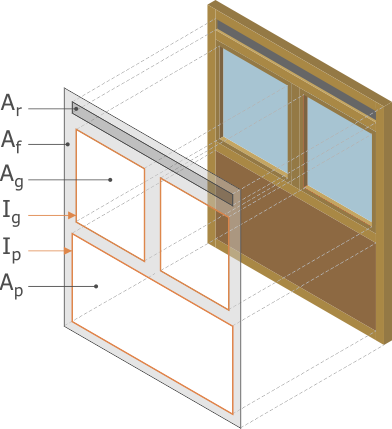
Une fenêtre ou une porte est constituée de différentes parties qui ont chacune une surface et un coefficient de transmission thermique U déterminés.

l’encadrement (châssis) de la fenêtre ou de la porte (dans tous les cas) ;
le ou les vitrages (le cas échéant) ;
le ou les panneaux opaques (le cas échéant) ;
la ou les grilles de ventilation (le cas échéant).

Le contour des vitrages isolants et des panneaux est affecté d’une déperdition thermique supplémentaire résultant des effets combinés des encadrements, intercalaires, vitrages et panneaux (pont thermique linéaire).

L’ensemble de ces éléments permet de déterminer par calcul le coefficient de transmission thermique de la fenêtre Uw. Il s’agit de la valeur moyenne des coefficients de transmission thermique des différentes parties au pro rata de leurs surfaces, augmentées des déperditions linéiques aux rives des vitrages et panneaux.

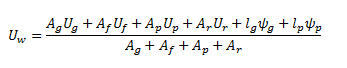
avec :

U_g = le coefficient de transmission thermique du vitrage
A_g = l’aire du vitrage
U_f = le coefficient de transmission thermique de l’encadrement
A_f = l’aire de l’encadrement
U_p = le coefficient de transmission thermique du panneau
A_p = l’aire du panneau
U_r = le coefficient de transmission thermique de la grille de ventilation
A_r = l’aire de la grille de ventilation
ψ_g = le coefficient de transmission thermique linéique de l’intercalaire autour du vitrage
l_g = le périmètre visible du vitrage
ψ_p = le coefficient de transmission thermique linéique autour du panneau
l_p = le périmètre visible du panneau

Le calcul doit être effectué pour chaque fenêtre et porte.

Calcul simplifié

Pour un ensemble de fenêtres ayant un même type de vitrage, d’encadrement, de panneau de remplissage opaque et de grille de ventilation, et étant placées dans le même bâtiment, on peut adopter une seule valeur moyenne UW pour l’ensemble des fenêtres. Celle-ci tient compte d’une proportion fixe entre l’aire du vitrage et l’aire de l’encadrement ainsi que d’un périmètre du vitrage ou des intercalaires. On évite ainsi de devoir faire ce calcul pour chaque fenêtre.

La réglementation PEB fournit ainsi une formule simplifiée permettant d’évaluer l’efficacité énergétique d’une fenêtre en tenant compte de l’efficacité du châssis et du vitrage tout en supposant une bonne étanchéité à l’air.

		Partie vitrage et encadrement	Partie grille de ventilation
U_g ≤ U_f	U_w	= 0,7U_g + 0,3U_f + 3ψ_g	+ ∑A_r (U_r – U_g)/∑A_W,d	[W/m²K]
U_g > U_f	U_w	= 0,8U_g + 0,2Uf + 3ψ_g	+ ∑A_r (U_r – U_f)/∑A_W,d	[W/m²K]

avec :

U_vc = coefficient de transmission thermique U du vitrage.
U_ch = coefficient de transmission thermique U du châssis.
ψ_g= coefficient de transmission thermique linéique de l’intercalaire.
U_r = coefficient de transmission thermique de la grille de ventilation
∑A_r = aire totale des grilles de ventilation présentes
∑A_W,d = aire totale des fenêtres (déterminée sur la base des aires des baies des fenêtres)

La proportion varie suivant que le vitrage est thermiquement plus performant que l’encadrement, ou l’inverse. Généralement c’est le vitrage qui est le plus performant. Dans ce cas la formule de calcul devient, s’il n’y a ni grille ni panneau :

U_W,T= 0,7 U_g+0,3 U_f+3 ψ_g

Ce qui revient à considérer : 70 % de vitrage, 30 % d’encadrement et 3 m d’intercalaire par m² de fenêtre.

Si la fenêtre comprend des grilles de ventilation et des panneaux opaques la formule se complique. Elle tient compte de l’influence de ces éléments sur le résultat final (pour les calculs, se référer aux formules 20 et 21 de l’Art 8.5 de l’Annexe 7).

Source : AGW du 15 mai 2014, Annexe B1, Art 8.5

L’influence du volet (Uws)

En été, la présence d’un volet à l’extérieur améliore les moyens dont dispose le bâtiment pour résister à la surchauffe.

En hiver, un volet placé à l’extérieur d’une fenêtre apporte une résistance thermique supplémentaire lorsqu’il est fermé. Bien sûr, il n’est pas fermé en permanence et le taux de fermeture variera d’une fenêtre à l’autre. La législation PEB en Belgique suppose qu’il sera fermé 8 heures par jour.

La résistance thermique de l’ensemble fenêtre-volet s’exprime de la manière suivante :

R_ws = R_w + ΔR

ΔR dépendra de deux caractéristiques :

La résistance thermique totale du volet lui-même, R_sh ;
La fente totale effective entre les bords du volet et les bords de l’ouverture du jour de la fenêtre b_sh = b₁ + b₂ + b₃ . b₁, b₂ et b₃ sont respectivement la moyenne des ouvertures des fentes en bas, en haut et sur les côtés du volet.

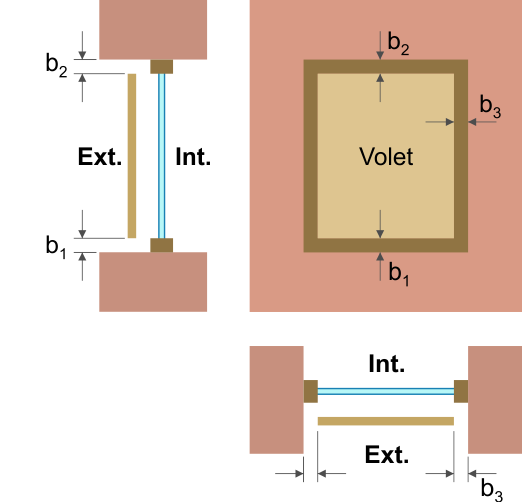
Attention, la fente sur le côté du volet (b3) n’est comptée qu’une fois parce que les fentes situées dans le haut et dans le bas ont une plus grande influence.

R_sh est calculé de la même manière que les autres éléments de construction.

Cas particuliers :

Le calcul se fait suivant la norme NBN EN ISO 10211 dans le cas d’un volet à composition hétérogène ;
Le calcul se fait suivant la norme NBN EN ISO 10077-2 dans le cas d’un élément profilé ;
Rsh = 0 dans le cas d’un volet inconnu.

Lorsque R_sh et b_sh sont déterminées, ΔR est calculé à partir des formules reprises dans le tableau 3 extrait de l’Art. 8.4.5 de l’Annexe B1 de l’AGW du 15 mai 2014.

Classe	Perméabilité à l’air du volet en position fermée	b_sh [mm]	ΔR [m²K/W]⁽¹⁾
1	Perméabilité très élevée	35 < b_sh	0,08
2	Perméabilité élevée (le volet est lui-même étanche à l’air).	15 < b_sh < 35	0,25 . R_sh + 0,09
3	Perméabilité moyenne (le volet est lui-même étanche à l’air)	8 < b_sh < 15	0,55 . R_sh + 0,11
4	Perméabilité faible (le volet est lui-même étanche à l’air).	b_sh < 8	0,80 . R_sh + 0,14
5	Perméabilité très faible (le volet est lui-même étanche à l’air).	b_sh < 3 et b₁ + b₃ = 0 ou₍₂₎ b₂₍₃₎ + b₃ = 0	0,95 . R_sh + 0,17
⁽¹⁾Les valeurs ΔR sont valables pour R_sh < 0,3 m²K/W (R_sh est la résistance thermique du volet même, déterminée selon le chapitre 6 si celui-ci est d’application, selon la NBN EN ISO 10211 dans le cas d’un volet à composition hétérogène ou selon la NBN ISO 10077-2 dans le cas d’un élément profilé). ⁽²⁾Ce cas suppose la présence de joints d’étanchéité autour d’au moins 3 côtés du volet et que du côté restant la fente soit inférieure ou égale à 3 mm. ⁽³⁾La classe 5 (perméabilité très faible) peut également être adoptée si une mesure du débit d’air au travers du volet fermé démontre que ce débit d’air n’est pas supérieur à 10 m³/h.m² (avec une différence de pression de 10 Pa – essai selon la NBN EN 12835. Des conditions supplémentaires pour la classe 5 sont disponibles dans la NBN EN 13125 par type de volet.

Tableau 3 : résistance thermique additionnelle de la couche d’air et du volet fermé.

ΔR étant ainsi connu, la résistance thermique de l’ensemble fenêtre volet Rws peut être calculée.
Le coefficient de conductivité thermique U_ws est finalement obtenu par la formule :

U_ws = 1 / R_ws

Le logiciel PEB permet de calculer automatiquement U_ws à partir des informations introduites.

Les caisses à volets roulants

Attention, la pose de volets suppose dans certains cas la présence de caisses à volets. Lorsqu’elles sont encastrées dans la façade, il faudra être très attentif à maintenir la continuité de la couche isolante et l’étanchéité à l’air du bâtiment. Cela n’est pas toujours facile. Les détails techniques doivent être étudiés avec soin dès de le début de la conception de l’immeuble.

Source: AGW du 15 mai 2014, Annexe B1, Art 8.4.5

Posted By : olivier 24 Mar, 2011

Coefficient de transmission thermique d’une paroi (U)

Généralités

Le coefficient de transmission thermique d’une paroi est la quantité de chaleur traversant cette paroi en régime permanent, par unité de temps, par unité de surface et par unité de différence de température entre les ambiances situées de part et d’autre de la paroi.
Le coefficient de transmission thermique est l’inverse de la résistance thermique totale (R_T) de la paroi.

U = 1 / R_T

> U (ou k) s’exprime en W/m²K
Plus sa valeur est faible et plus la construction sera isolée.

Pour calculer le coefficient U d’une paroi, rendez-vous sur la page « Calculs » – catégorie « Enveloppe » !

Posted By : olivier 24 Mar, 2011

Résistance thermique d’échange superficiel d’une paroi (Rsi et Rse)

La transmission de la chaleur de l’air ambiant à une paroi et vice versa se fait à la fois par rayonnement et par convection.

…..

Le coefficient d’échange thermique superficiel entre une ambiance intérieure (h_i) et une paroi est la somme des quantités de chaleur transmise entre une ambiance intérieure et la face intérieure d’une paroi, par convection et par rayonnement, par unité de temps, par unité de surface de la paroi, et pour un écart de 1 K entre la température de la résultante sèche de l’ambiance et la température de surface.

> h_i s’exprime en W/m²K.

La résistance thermique d’échange d’une surface intérieure (R_si) est égale à l’inverse du coefficient d’échange thermique de surface intérieure h_i_.

R_si= 1/h_i

> R_si s’exprime en m²K/W.

Le coefficient d’échange thermique superficiel entre une paroi et une ambiance extérieure (h_e) est la somme des quantités de chaleur transmise entre la face extérieure d’une paroi et une ambiance extérieure, par convection et par rayonnement, par unité de temps, par unité de surface de la paroi, et pour un écart de 1 K entre la température de la résultante sèche de l’ambiance et la température de surface.

> h_e s’exprime en W/m²K.

La résistance thermique d’échange d’une surface extérieure (R_se) est égale à l’inverse du coefficient d’échange thermique de surface extérieure h_e_.

R_se= 1/h_e

> R_se s’exprime en m²K/W.

Les différences de valeur entre R_si et R_se ne proviennent pas de la différence de température entre l’intérieur et l’extérieur mais bien des mouvements d’air plus importants à l’extérieur qu’à l’intérieur, ce qui influence le transfert de chaleur par convection.

Les valeurs des résistances thermiques d’échange superficiel R_i et R_e sont données dans un tableau extrait de la réglementation thermique.

Posted By : olivier 24 Mar, 2011

Résistance thermique d’une couche d’air (Ra)

Définition d’une couche d’air

Pour qu’un espace vide situé à l’intérieur d’une paroi soit considérée comme une couche d’air, dans le cadre de la réglementation, il faut que les conditions suivantes soient remplies (source : Annexe VII de l’AGW du 17 avril 2008, Art. 5.4.2.1):

la couche d’air doit être délimitée par deux plans parallèles qui sont perpendiculaires à la direction du flux thermique ;
les deux faces de ces plans sont non-réfléchissants (c’est le cas de la plupart des matériaux de construction traditionnels)¹ ;
l’épaisseur de la couche d’air ne peut dépasser 30 cm ;
l’épaisseur de la couche d’air doit 10 fois plus petite que sa longueur et sa largeur ;
il ne peut pas y avoir de passage d’air entre la couche d’air et l’environnement intérieur du bâtiment².

¹Si une des couche au moins est réfléchissante, il faut se référer aux annexes B.2 et B.3 de la NBN EN ISO 6946.
²Dans le cas contraire, la couche d’air et toutes les couches de matériaux situés du côté intérieur par rapport à celle-ci, ne sont pas pris en considération.

R_a, la résistance thermique d’une couche d’air plane est l’inverse de la quantité de chaleur qui est transmise en régime permanent de la face chaude de la couche d’air vers la face froide, par conduction, convection et rayonnement, par unité de temps, par unité de surface et pour un écart de 1 K entre les températures des faces chaudes et froides.

> R_a s’exprime en m²K/W.

Définition d’une couche d’air non-ventilée

Une couche d’air sera considérée comme « non-ventilée » lorsque la surface des ouvertures entre cette couche d’air et l’environnement extérieur ne dépasse pas 5 cm²

par m de longueur dans le cas d’une paroi verticale ou
par m² de surface dans le cas d’une paroi horizontale³.

³Une paroi inclinée sera considérée comme verticale dès que sa pente dépasse 30°. Dans le cas contraire, elle sera considérée comme horizontale.

NB : Une paroi inclinée sera considérée comme verticale dès que sa pente dépasse 30°. Dans le cas contraire, elle sera considérée comme horizontale.

Les résistances thermiques des couches d’air non ventilées R_a sont données dans un tableau extrait de la réglementation thermique en fonction de l’épaisseur de la lame d’air et de la direction du flux.

Définition d’une couche d’air peu ventilée

Une couche d’air sera considérée comme « peu ventilée » lorsque la surface des ouvertures entre cette couche d’air et l’environnement extérieur est comprise entre 5 cm² et 15 cm²

par m de longueur dans le cas d’une paroi verticale ou
par m² de surface dans le cas d’une paroi horizontale (pente<30°).

Dans ce cas, on peut considérer pour cette couche une résistance thermiques R_a correspondant à la moitité de celle donnée pour une couche d’air non-ventilée d’épaisseur équivalente. De plus, la résistance thermique globale prise en compte pour les couches de construction entre la couche d’air et l’environnement extérieur sera limitée à maximum 0,15 m²K/W.

Définition d’une couche d’air fortement ventilée

Une couche d’air sera considérée comme « fortement ventilée » lorsque la surface des ouvertures entre cette couche d’air et l’environnement extérieur dépasse plus de 15 cm²

par m de longueur dans le cas d’une paroi verticale ou
par m² de surface dans le cas d’une paroi horizontale (pente<30°).

Dans ce cas, on considère pour cette couche une résistance thermique R_a nulle et la valeur R_si sera utilisée comme valeur caractéristique de la résistance thermique d’échange superficiel extérieur (R_se=R_si).

Posted By : olivier 24 Mar, 2011

Résistance thermique d’une couche de matériau (R)

La perméance thermique d’une couche de matériau

La perméance thermique (P) indique la quantité de chaleur qui se propage :

en 1 seconde,
à travers 1 m² d’une couche de matériau,
d’une épaisseur déterminée,
lorsque la différence de température entre les deux faces est de 1 K (1 K = 1 °C).

> La perméance thermique s’exprime en W/m²K.

Plus la perméance thermique est élevée, plus la couche laisse passer la chaleur.
Ce coefficient est valable aussi bien pour les matériaux homogènes que pour les matériaux non-homogènes.

Matériau homogène : P = λ / d où d = épaisseur de la paroi.
Matériau non-homogènes : P est déduite d’essais effectués en laboratoire.

La résistance thermique d’une couche de matériau

La notion de perméance thermique est peu utilisée. Elle permet d’introduire et de mieux comprendre la résistance thermique (R) qui est l’inverse de la perméance thermique.

R = 1 / P

> Elle s’exprime en m²K/W.

C’est la mesure de performance isolante de la couche de matériau. Plus la résistance thermique est élevée, plus la couche est isolante.
Ce coefficient est valable aussi bien pour les matériaux homogènes que pour les matériaux non homogènes.

Matériau homogène

La résistance thermique est obtenue par le rapport entre l’épaisseur (en m) et la conductivité thermique de la couche du matériau (en W/m.K) :

R = d / λ

Matériau non-homogène

La résistance thermique utile R_uest déduite d’essais effectués en laboratoire.

La valeur déclarée

La valeur déclarée R_D d’une couche de matériau de construction est généralement fournie par son fabricant. Cette valeur est certifiée sur base d’un agrément technique (ATG, CE, ETA, ETZ, …). Elle est obtenue dans des conditions de référence données de température et d’humidité (d’après les principes donnés dans la EN ISO 10456).

Les valeurs de calcul

À partir de cette valeur R_D, il est possible de déduire les valeurs de calcul de la conductivité thermique R_U,i et R_U,e qui correspondent aux conditions d’utilisation du matériau (interne ou externe).

Il existe un site officiel ( www.epbd.be) qui indique, pour les trois régions belges, les valeurs R_U,i et R_U,e de certains matériaux qui peuvent être utilisées pour le calcul des performances thermiques des parois suivant la réglementation PEB.

Les valeurs de calcul par défaut

Des valeurs de calcul R_U,i par défaut peuvent toujours être utilisées lorsque le matériau ne possède pas de valeur R_D certifiée ou n’est connu que par sa nature. Ces valeurs sont reprises dans un tableau de la réglementation.

La résistance thermique d’une couche de matériau homogène d’épaisseur variable

Dans les parois de l’enveloppe du volume protégé, certaines couches peuvent avoir des épaisseurs variables.

Exemples :

Un béton de pente
(peu d’influence sur la résistance thermique totale).

Une couche d’isolant à épaisseur variable
(grande influence sur la résistance thermique totale).

Méthode simplifiée

La résistance thermique de cette couche peut être déterminée de manière sécuritaire en considérant que son épaisseur est partout égale à son épaisseur la plus faible d_min -> R = d_min/λ.

Épaisseur d_min

Méthode précise

Si la différence de pente entre les deux faces de la couche est inférieure à 5 %, une méthode de calcul existe pour quantifier avec plus de précision les performances thermiques de la paroi. Celle-ci est décrite dans l’Annexe B1 de l’AGW du 15 mai 2014 à l’Art. 7.4.

Elle consiste à décomposer la paroi en éléments partiels de formes déterminées et à calculer à l’aide de formules directement la valeur U de chacun de ces éléments.

Décomposition de la paroi en éléments partiels.

Les formes de base :

Rectangulaire

U = 1/R₁. ln [1 + R₁/R₀]

Triangulaire avec partie la plus épaisse à la pointe

U = 2/R₁. [(1 + R₀/R₁) . ln (1+R₁/R₀) – 1]

Triangulaire avec partie la plus mince à la pointe

U = 2/R₁. [1 – R₀/R₁ . ln (1+R₁/R₀)]

Avec :

R₁: Résistance thermique maximale de la couche inclinée
R₀: Résistance thermique globale de l’élément d’environnement à environnement sans R₁.

Un outils de calcul développé par l’IBGE existe et est disponible ici. XLS

Si par contre, la différence de pente entre les deux faces de la couche est supérieure à 5%, cette méthode ne s’applique pas et un calcul numérique doit être réalisé.

La résistance thermique d’une couche de mousse de polyuréthane (PUR) projetée in situ

Il est difficile d’évaluer l’épaisseur exacte d’une couche de mousse de polyuréthane projetée in situ.

PUR projeté.

C’est la raison pour laquelle la résistance thermique R de cette couche est multipliée par un terme correctif a qui varie en fonction du type d’application.

R _{PUR projeté} = a x R _{PUR en plaque}

a vaut 0.85 pour les applications en toiture.
a vaut 0.925 pour les applications sur sol.

Source: AGW du 15 mai 2014, Annexe B1, Art 7. 3

PUR projeté en toiture.

PUR projeté sur sol.

La résistance thermique d’une couche de maçonnerie

Une maçonnerie est constitué de briques ou de blocs assemblés et solidarisés entre eux par du mortier. La résistance thermique d’une couche de maçonnerie devra donc prendre en compte l’épaisseur de ce joint de mortier.

Si cette épaisseur est inférieure à 3 mm, on peut considérer que les briques ou blocs sont collés. Dans ce cas, le coefficient de conductivité thermique utile λ_U de la maçonnerie est égal à celui des briques ou blocs. La résistance thermique de la couche est donc égale à l’épaisseur de la maçonnerie divisée par le coefficient de conductivité thermique de la brique ou du bloc.

R = d_U,maç / λ_{U,brique/bloc}

Blocs collés.

Si cette épaisseur est supérieure à 3 mm, il faudra tenir compte de la présence des joints pour déterminer le coefficient de conductivité thermique λ_U moyen de la maçonnerie.

λ_U,moyen = (λ_{U,brique/bloc} x Surface _brique/bloc + λ_U,jointx Surface _joint) / Surface _totale

Surface_joint = (l + h + d) x d
Surface_brique/bloc = l x h
Surface_totale = (l + d) x (h + d)

La résistance thermique de la couche est donc égale à l’épaisseur de la maçonnerie divisée par le coefficient de conductivité thermique moyen.

R = d_maç / λ_U,moyen

Valeurs par défaut

Lorsque la proportion de joints n’est pas connue,

si la conductivité thermique des joints est inférieure à des biques ou blocs, on peut considérer la maçonnerie comme collée (donc sans joints) ;
si la conductivité thermique des joints est supérieure à des biques ou blocs, on peut considérer :
- la fraction joints égale à 16 % pour les maçonneries intérieures et
- la fraction joints égale à 28 % pour les maçonneries extérieures.

Source: AGW du 15 mai 2014, Annexe B1, Art. G.3.1

La résistance thermique d’une couche non homogène d’un élément de construction avec structure bois

Les parois du volume protégé peuvent contenir des couches de matériaux non-homogènes dans lesquelles une structure bois est incorporée et dont le reste de l’espace est occupé par un matériau isolant.

Exemples :

chevrons d’une toiture inclinée ;
gîtage d’une toiture plate, d’un plafond ou d’un plancher en bois;
structure d’une façade légère à ossature bois ;
…

Façades et plancher à ossature bois.

Toit incliné à chevrons.

Cette structure affaiblit le pouvoir isolant de la couche. Il faut donc en tenir compte pour en calculer la résistance thermique.

Celle-ci dépend de la fraction bois. Dans le cas d’une structure régulière, la fraction bois est égale à la largeur des éléments en bois divisée par la distance moyenne entre les éléments (d’axe en axe).

% bois = d / l moyen

Cette fraction est généralement augmentée de 1 % pour tenir compte des entretoises.

Calcul de la résistance thermique de la couche

La résistance thermique de la couche se calcule donc en utilisant un coefficient de conductivité thermique λ_U moyen.

λ_U,moyen = λ_U,bois x % bois + λ_U,isolant x (100 % – % bois)

La résistance thermique de la couche est donc égale à l’épaisseur de la couche divisée par le coefficient de conductivité thermique moyen.

R = d / λ_U,moyen

Valeurs par défaut

La réglementation propose l’utilisation de valeurs par défaut. Elles correspondent aux limites supérieures des valeurs les plus courantes en fonction du type de paroi. Celles-ci sont reprises dans le tableau suivant :

Structure en bois	Fraction de bois (valeur par défaut)
Toiture à pannes (pannes-structure portante primaire)	0,11
Toiture à pannes (chevrons-structure portante secondaire)	0,20
Toiture à fermes (fermettes-structure portante secondaire)	0,12
Planchers en bois (poutres-structure portante secondaire)	0,11
Parois à ossature en bois	0,15

Source: AGW du 15 mai 2014, Annexe B1, Art G.4

Daily Archives: 24 mars 2011

Coefficient de transmission thermique d’une fenêtre (Uw) ou d’une porte

Le coefficient de transmission thermique d’une fenêtre ou d’une porte simple

Détermination par essais

Détermination par calcul

Calcul simplifié

L’influence du volet (Uws)

Les caisses à volets roulants

Coefficient de transmission thermique d’une paroi (U)

Généralités

Résistance thermique d’échange superficiel d’une paroi (Rsi et Rse)

Résistance thermique d’une couche d’air (Ra)

Définition d’une couche d’air

Définition d’une couche d’air non-ventilée

Définition d’une couche d’air peu ventilée

Définition d’une couche d’air fortement ventilée

Résistance thermique d’une couche de matériau (R)

La perméance thermique d’une couche de matériau

La résistance thermique d’une couche de matériau

Matériau homogène

Matériau non-homogène

La valeur déclarée

Les valeurs de calcul

Les valeurs de calcul par défaut

La résistance thermique d’une couche de matériau homogène d’épaisseur variable

Méthode simplifiée

Méthode précise

La résistance thermique d’une couche de mousse de polyuréthane (PUR) projetée in situ

La résistance thermique d’une couche de maçonnerie

Valeurs par défaut

La résistance thermique d’une couche non homogène d’un élément de construction avec structure bois

Calcul de la résistance thermique de la couche

Valeurs par défaut